サッカーは無数のディテール(詳細)であふれている。重箱の隅をつつくような、「超マニアックコラム」。今回は、「エリア前の変な物」。サッカージャーナリスト大住良之が、歴史と算数に挑む。
「ペナルティーアーク」の詳細に戻ろう。円の一部に交わる直線を「割線」と呼ぶが、この割線が円弧と交わる2点を結んだ線は「弦」と呼ばれる。「弧」と「弦」の長さ、そしてこの2つの線で囲まれた「弓形」の面積は、ペナルティースポットと「ペナルティーアーク」の両端を結んだ「扇形」の「中心角」を分度器を使って測れば、小学生でも近い数字までたどり着けるはずである。ただ、少し高度な数学を使えば、円の半径と「弓形」の高さ(「矢高」と言うらしい)のデータだけで計算できる。
と書いたが、残念ながら私がスラスラとこの問題を解いたわけではない。いまはネットで『高度計算サイト』という便利なものがあり、そこに半径と「矢高」のデータを入力して「計算」のボタンをポンと押せば、たちまちにして小数点何ケタまででも結果が出るという仕掛けである。
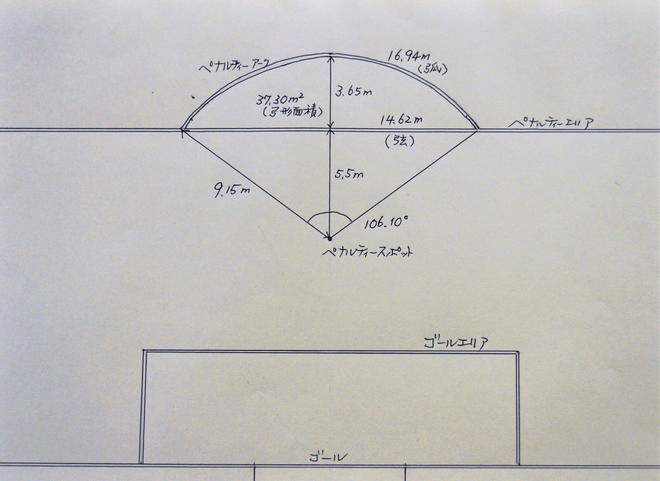
半径は9.15メートルである。ペナルティースポットからペナルティーエリアまでの距離は5.5メートルだから、「矢高」は明らかで、3.65はメートルとなる。この2つのデータで計算すると、「弧」の長さは16.94メートル(小数点2ケタまでの数字。以下同)、「弦」の長さは14.62メートル、そして「弓形」の面積は37.30平方メートルである。
ちなみに、中心角は106.10度だそうだ。画用紙にせっせと図を書き、『ダイソー』で買った分度器を使って私が測ったところ、中心角は「106.4度」だった。これを元に計算した「弧」の長さは16.98メートルで、「弦」は14.6メートル(これはものさしで測った)、「弓形」の面積は37.55平方メートルだったから、「小学生の算数」を馬鹿にしてはならないというところだろうか。
それにしても、「37.30平方メートル」という数字を見て、私はうなってしまった。6月にU-24日本代表となでしこジャパンのオリンピック前の親善試合を取材するために京都で宿泊したホテルの部屋の広さは、たしか11平方メートルあたりではなかっただろうか。そして資料や本の山を積み上げ、その間を縫うように歩いている東京の仕事場も、ピッチの上ではあんなに小さく見える「ペナルティーアーク」の弓形の面積とどっこいどっこいではないか。ペナルティーアークがつくる弓形は、平均的な「2K」のアパートよりも広いのである。








